A distribuição Beta é uma distribuição de probabilidade contínua definida no intervalo [0, 1] e caracterizada por dois parâmetros de forma, α (alfa) e β (beta), ambos maiores que zero. Essa distribuição é extremamente versátil e amplamente utilizada em diversas áreas, desde estatística Bayesiana e modelagem de eventos aleatórios até controle de qualidade e análise de risco. Em Python, a distribuição Beta pode ser facilmente implementada e manipulada através de bibliotecas como SciPy, tornando-a uma ferramenta poderosa para cientistas de dados, estatísticos e engenheiros.

Este artigo tem como objetivo explorar a distribuição Beta em Python, abordando seus fundamentos teóricos, aplicações práticas e exemplos de código utilizando a biblioteca SciPy. Nosso foco será em fornecer um guia completo para entender e utilizar a distribuição Beta, com ênfase em exemplos práticos e relevantes para o dia a dia.

Fundamentos Teóricos da Distribuição Beta

A função de densidade de probabilidade (PDF) da distribuição Beta é dada por:

f(x; α, β) = (x^(α-1) * (1-x)^(β-1)) / B(α, β)

onde:

* `x` é a variável aleatória, representando um valor entre 0 e 1.

* `α` é o primeiro parâmetro de forma, controlando a concentração da distribuição em torno de valores próximos de 1.

* `β` é o segundo parâmetro de forma, controlando a concentração da distribuição em torno de valores próximos de 0.

* `B(α, β)` é a função Beta, também conhecida como integral Beta, que serve como um fator de normalização para garantir que a integral da PDF seja igual a 1. A função Beta é definida como:

B(α, β) = ∫[0,1] t^(α-1) * (1-t)^(β-1) dt = Γ(α) * Γ(β) / Γ(α + β)

onde `Γ` é a função Gama.

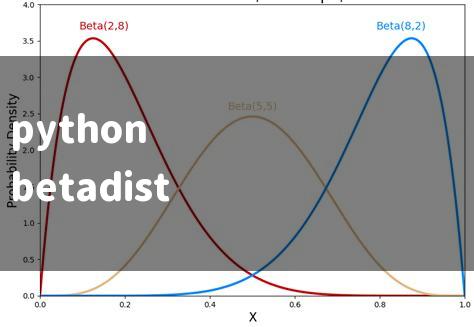
Os parâmetros α e β desempenham um papel crucial na determinação da forma da distribuição Beta. Diferentes combinações de α e β resultam em distribuições com características distintas:

* α > 1 e β > 1: A distribuição é unimodal (tem um único pico) e concentrada em torno de um valor intermediário entre 0 e 1.

* α < 1 e β < 1: A distribuição é bimodal (tem dois picos), com alta probabilidade em torno de 0 e 1.

* α > 1 e β < 1: A distribuição é assimétrica, com maior concentração em torno de 1.

* α 1: A distribuição é assimétrica, com maior concentração em torno de 0.

* α = β = 1: A distribuição Beta se torna uma distribuição uniforme no intervalo [0, 1].

Aplicações da Distribuição Beta

A distribuição Beta encontra aplicações em uma ampla gama de áreas, incluindo:

* Estatística Bayesiana: A distribuição Beta é frequentemente utilizada como distribuição a priori para parâmetros de probabilidade em modelos Bayesianos. Por exemplo, pode ser usada como a priori para a probabilidade de sucesso em um processo de Bernoulli.

* Modelagem de Eventos Aleatórios: A distribuição Beta pode ser usada para modelar a probabilidade de um evento ocorrer, especialmente quando há informações prévias sobre a probabilidade. Por exemplo, pode ser usada para modelar a probabilidade de um cliente clicar em um anúncio online.

* Controle de Qualidade: A distribuição Beta pode ser usada para modelar a proporção de itens defeituosos em um lote de produção.

* Análise de Risco: A distribuição Beta pode ser usada para modelar a probabilidade de um evento de risco ocorrer, como a probabilidade de um projeto ser concluído dentro do prazo ou a probabilidade de um investimento gerar um retorno positivo.

* Aprendizado de Máquina: A distribuição Beta pode ser usada para modelar a confiança em um modelo de aprendizado de máquina.

Python Beta Example: Implementação com SciPy